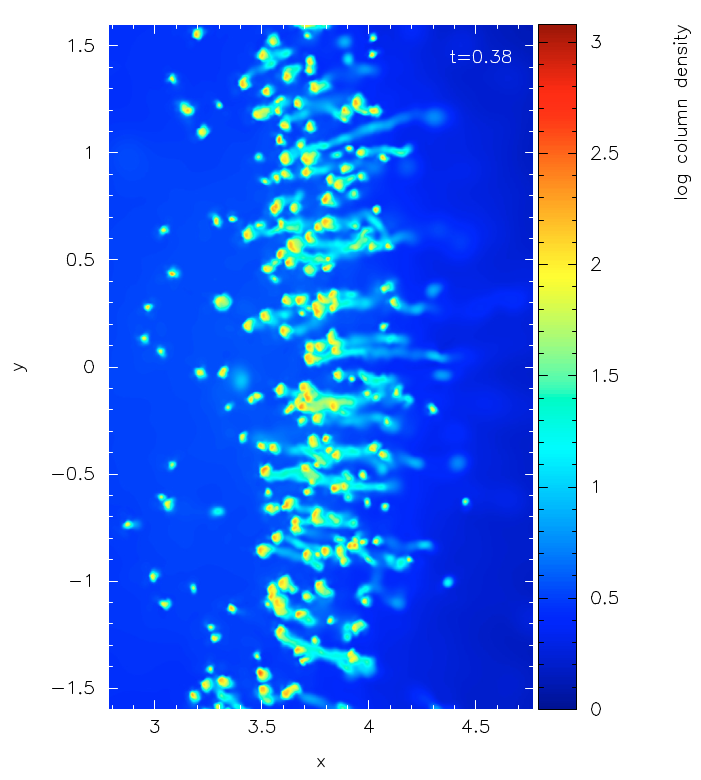
Massive stars emit copious amount of photons that are able to ionize the atom of hydrogen in their nearby environment of the interstellar medium (ISM). This influence of UV radiation on the ambient ISM is of great interest. As this radiation ionizes the surrounding neutral material, it creates a region of hot ionized gas, known as an “HII region”. The huge contrast in pressure between the ionized gas in the HII region and the surrounding neutral gas causes the HII region to expand and sweep up the neutral gas into a dense shell. This dense shell is likely to be prone to many different instabilities an some of these instabilities may trigger fragmentation and star-formation. This mode of star-formation is usually referred to as the “collect and collapse” mechanism.
The problem of the expansion of an HII region into a uniform neutral medium has a long history in theoretical and numerical studies of the ISM. The photoionized region is bounded by an ionization front, which separates the ionized from the neutral gas. Around 70 years ago, Kahn (1954) and Axford (1961) have shown analytically that the ionization front relatively quickly switches from R-type to D-type and drives a strong shock in the neutral ISM. The analytical solution proposed by Spitzer (1978) and Dyson & Williams (1980) has become the standard solution used in theoretical approaches and with which numerical results are compared.
I have written a algorithm in Smoothed Particle Hydrodynamics which is able to propagate the ionizing radiation emitted by a hypothetical massive star and which can simulate an expanding HII region in a three-dimensional arbitrary density distribution. Using this code, I have studied triggered star formation in a mode called “radiation driven implosion” and found a criterion that can estimate whether star-formation can occur in an observed clump that is irradiated externally. in addition, I have participated in a team that has re-structured the analytical approach of an expanding HII region and found a solution that is more accurate than the solutions proposed by Spitzer (1978) and Dyson & Williams (1980).
