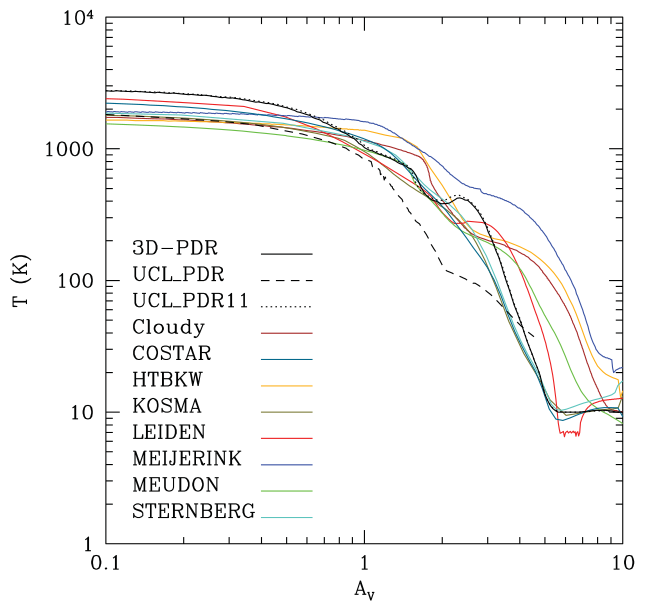
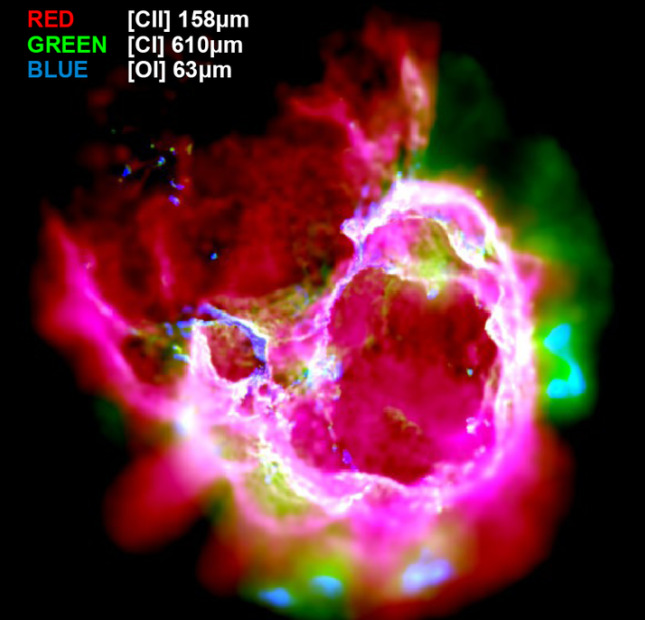
Photodissociation regions (PDRs) are ubiquitously present in the interstellar medium (ISM) and consist of predominantly neutral gas and dust illuminated by far-ultraviolet (FUV) radiation (6 < hv < 13.6 eV). Studies of PDRs allow us to understand the effects of FUV photons on the chemistry and structure of the neutral ISM in galaxies, as well as diagnosing the conditions within star-forming regions. PDRs are responsible for most of the infrared radiation from galaxies. Solving numerically the astrochemical network that occurs in PDRs is a powerful way to estimate the abundances of species and simulate the line emission of the observed galactic and extragalactic clouds.
I am the main developer of the astrochemical code 3D-PDR. This is an open-source OpenMP-parallelized 3D code. It is specifically designed to treat PDRs of arbitrary density distributions. It uses the Large Velocity Gradient approximation to compute the cooling functions, using a HEALPIX-based ray-tracing scheme. The code solves for the thermal balance self-consistently with the chemistry, to determine the gas temperature. It includes heating due to photoionisation and photodissociation reactions, in addition to the standard gas-phase chemistry and it accounts for self-shielding of H2 and CO against photodissociation. Suprathermal formation of CO via CH+ is included.
Together with Dr. T. Haworth, we embedded 3D-PDR in the photoionisation-hydrodynamics code TORUS, creating the MPI-parallelized TORUS-3DPDR hydro-photochemical code. The tool is able to perform photoionisation calculations using an iterative Monte Carlo photon packet propagating routine. It can calculate complicated 3D UV radiation fields from single or multiple sources, including their diffuse component of the radiation field. TORUS-3DPDR is therefore able to simulate -for the first time- HII/PDR complexes of arbitrary density distributions. This makes it superior to synthetic observations obtained by post-processing hydrodynamical simulations and allows for directly making the important connection between the numerical and observational data cubes.
